It is important to realize that the use of
trigonometry here is unhistorical: Archimedes
did not have the advantage of an algebraic and trigonometrically notation
and had to derive (1) and (2) by purely geometrical means. Moreover he
did not even have the advantage of our decimal notation for numbers, so
that the calculation of a6 and b6
from (1) and (2) was by no means a trivial task. So it was a pretty
stupendous feat both of imagination and of calculation and the wonder is
not that he stopped with polygons of 96 sides, but that he went so far.
For of course there is no reason in principle why one should not go
on. Various people did, including:
Except for Tsu
Ch'ung Chi, about whom next to nothing is known and who is very unlikely
to have known about Archimedes'
work, there was no theoretical progress involved in these improvements,
only greater stamina in calculation. Notice how the lead, in this as in
all scientific matters, passed from Europe to the East for the
millennium 400 to 1400 AD.
Al-Khwarizmi
lived in Baghdad, and incidentally gave his name to 'algorithm', while
the words al jabr in the title of one of his books gave us the
word 'algebra'. Al-Kashi
lived still further east, in Samarkand, while Tsu
Ch'ung Chi, one need hardly add, lived in China.
The European Renaissance brought about in due course
a whole new mathematical world. Among the first effects of this
reawakening was the emergence of mathematical formulae for 
.
One of the earliest was that of Wallis
(1616-1703)
2/ = (1.3.3.5.5.7.
...)/(2.2.4.4.6.6. ...)
and one of the best-known is
/4 = 1 - 1/3
+ 1/5 - 1/7 + ....
This formula is sometimes attributed to Leibniz
(1646-1716) but is seems to have been first discovered by James Gregory
(1638- 1675).
These are both dramatic and astonishing formulae, for the expressions
on the right are completely arithmetical in character, while
arises in the first instance from geometry. They show the surprising
results that infinite processes can achieve and point the way to the
wonderful richness of modern mathematics.
From the point of view of the calculation of ,
however, neither is of any use at all. In Gregory's
series, for example, to get 4 decimal places correct we require the
error to be less than 0.00005 = 1/20000, and so we need about 10000
terms of the series. However, Gregory
also showed the more general result
(3) . . . tan-1 x = x - x3/3
+ x5/5 - ... (-1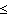 
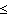x 1)
from which the first series results if we put x = 1. So using the fact
that
tan-1(1/
3)
= /6
we get
/6 = (1/3)(1
- 1/(3.3) + 1/(5.3.3) - 1/(7.3.3.3) + ...
which converges much more quickly. The 10th term is 1/19 
393,
which is less than 0.00005, and so we have at least 4 places correct
after just 9 terms.
An even better idea is to take the formula
(4) . . . /4
= tan-1(1/2) + tan-1(1/3)
and then calculate the two series obtained by putting first 1/2
and the 1/3 into (3).
Clearly we shall get very rapid convergence indeed if we can find a
formula something like
/4 = tan-1(1/a)
+ tan-1(1/b)
with a and b large. In 1706 Machin found such a formula:
(5) . . . /4
= 4 tan-1(1/5) - tan-1(1/239)
Actually this is not at all hard to prove, if you know how to prove (4)
then there is no real extra difficulty about (5), except that the
arithmetic is worse. Thinking it up in the first place is, of course,
quite another matter.
With a formula like this available the only
difficulty in computing
is the sheer boredom of continuing the calculation. Needless to say, a
few people were silly enough to devote vast amounts of time and effort
to this tedious and wholly useless pursuit. One of them. an Englishman
named Shanks, used Machin's
formula to calculate
to 707 places, publishing the results of many years of labour in 1873.
Shanks has achieved immortality for a very curious reason which we shall
explain in a moment.
Here is a summary of how the improvement went.
| 1699: |
Sharp used Gregory's
result to get 71 correct digits |
| 1701: |
Machin used an improvement to get 100 digits and the following
used his methods:
|
| 1719: |
de Lagny found 112
correct digits
|
| 1789: |
Vega got 126 places and
in 1794 got 136 |
| 1841: |
Rutherford calculated 152 digits and in 1853 got 440
|
| 1873: |
Shanks calculated 707
places of which 527 were correct |
A more detailed a Chronology is
available.
Shanks
knew that was
irrational since this had been proved in 1761 by Lambert.
Shortly after Shanks'
calculation it was shown by Lindemann
that is
transcendental, that is,
is not the solution of any polynomial equation with integer
coefficients. In fact this result of Lindemann
showed that 'squaring the circle' is impossible. The transcendentality
of implies that
there is no ruler and compass construction to construct a square equal
in area to a given circle.
Very soon after Shanks'
calculation a curious statistical freak was noticed by De
Morgan, who found that in the last of 707 digits there was a
suspicious shortage of 7's. He mentions this in his Budget of
Paradoxes of 1872 and a curiosity it remained until 1945 when
Ferguson discovered that Shanks
had made an error in the 528th place, after which all his digits were
wrong. In 1949 a computer was used to calculate
to 2000 places. In this and all subsequent computer expansions the
number of 7's does not differ significantly from its expectation, and
indeed the sequence of digits has so far passed all statistical tests
for randomness.
You can see 2000 places of .
We should say a little of how the notation
arose. Oughtred in 1647 used
the symbol d/
for the ratio of the diameter of a circle to its circumference. David
Gregory (1697) used /r
for the ratio of the circumference of a circle to its radius. The first
to use with its
present meaning was an Welsh mathematician William Jones
in 1706 when he states 3.14159 andc. = .
Euler adopted the symbol in 1737
and it quickly became a standard notation.
We conclude with one further statistical curiosity
about the calculation of ,
namely Buffon's needle
experiment. If we have a uniform grid of parallel lines, unit distance
apart and if we drop a needle of length k < 1 on the grid, the
probability that the needle falls across a line is 2k/.
Various people have tried to calculate
by throwing needles. The most remarkable result was that of Lazzerini
(1901), who made 34080 tosses and got
= 355/113
= 3.1415929
which, incidentally, is the value found by Tsu
Ch'ung Chi. This outcome is suspiciously good, and the game is given
away by the strange number 34080 of tosses. Kendall and Moran comment
that a good value can be obtained by stopping the experiment at an
optimal moment. If you set in advance how many throws there are to be
then this is a very inaccurate way of computing .
Kendall and Moran comment that you would do better to cut out a large
circle of wood and use a tape measure to find its circumference and
diameter.
Still on the theme of phoney experiments, Gridgeman, in a paper which
pours scorn on Lazzerini and others, created some amusement by using a
needle of carefully chosen length k = 0.7857, throwing it twice, and
hitting a line once. His estimate for
was thus given by
2 0.7857
/ = 1/2
from which he got the highly creditable value of
= 3.1428. He was not being serious!
It is almost unbelievable that a definition of
was used, at least as an excuse, for a racial attack on the eminent
mathematician Edmund Landau in
1934. Landau had defined
in this textbook published in Göttingen in that year by the, now fairly
usual, method of saying that /2
is the value of x between 1 and 2 for which cos x
vanishes. This unleashed an academic dispute which was to end in Landau's
dismissal from his chair at Göttingen. Bieberbach,
an eminent number theorist who disgraced himself by his racist views,
explains the reasons for Landau's
dismissal:-
Thus the valiant rejection by the Göttingen
student body which a great mathematician, Edmund Landau,
has experienced is due in the final analysis to the fact that the
un-German style of this man in his research and teaching is unbearable
to German feelings. A people who have perceived how members of another
race are working to impose ideas foreign to its own must refuse
teachers of an alien culture.
G H Hardy
replied immediately to Bieberbach
in a published note about the consequences of this un-German definition
of
There are many of us, many Englishmen and many
Germans, who said things during the War which we scarcely meant and
are sorry to remember now. Anxiety for one's own position, dread of
falling behind the rising torrent of folly, determination at all cost
not to be outdone, may be natural if not particularly heroic excuses.
Professor Bieberbach's
reputation excludes such explanations of his utterances, and I find
myself driven to the more uncharitable conclusion that he really
believes them true.
Not only in Germany did
present problems. In the USA the value of
gave rise to heated political debate. In the State of Indiana in 1897
the House of Representatives unanimously passed a Bill introducing a
new mathematical truth.
Be it enacted by the General Assembly of the State of Indiana: It
has been found that a circular area is to the square on a line equal
to the quadrant of the circumference, as the area of an equilateral
rectangle is to the square of one side.
(Section I, House Bill No. 246, 1897)
The Senate of Indiana showed a little more sense and postponed
indefinitely the adoption of the Act!
Open questions about the number
- Does each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 each occur
infinitely often in ?
- Brouwer's question: In
the decimal expansion of ,
is there a place where a thousand consecutive digits are all zero?
- Is simply
normal to base 10? That is does every digit appear equally often in
its decimal expansion in an asymptotic sense?
- Is normal
to base 10? That is does every block of digits of a given length
appear equally often in its decimal expansion in an asymptotic
sense?
- Is normal
? That is does every block of digits of a given length appear
equally often in the expansion in every base in an asymptotic sense?
The concept was introduced by Borel
in 1909.
- Another normal question! We know that
is not rational so there is no point from which the digits will
repeat. However, if
is normal then the first million digits 314159265358979... will
occur from some point. Even if
is not normal this might hold! Does it? If so from what point? Note:
Up to 200 million the longest to appear is 31415926 and this appears
twice.
As a postscript, here is a mnemonic for the decimal expansion of .
Each successive digit is the number of letters in the corresponding
word.
How I want a drink, alcoholic of course, after
the heavy lectures involving quantum mechanics. All of thy geometry,
Herr Planck, is fairly
hard...:
3.14159265358979323846264...
You can see more about the history of
in the History topic: Squaring
the circle and you can see a Chronology
of how calculations of
have developed over the years.
Article by: J J O'Connor and E
F Robertson
Circle 
Cartesian equation: x2 + y2 = a2
or parametrically: x = a cos(t), y = a sin(t)
Polar equation: r = a
Click HERE
to see one of the Associated curves.
If your browser can handle JAVA code, click HERE
to experiment interactively with this curve and its associated curves.
The study of the circle goes back beyond recorded history. The
invention of the wheel is a fundamental discovery of properties
of a circle.
The greeks considered the Egyptians as the inventors of geometry. The
scribe Ahmes, the author of the Rhind papyrus, gives a
rule for determining the area of a circle which corresponds to =
256/81 or approximately 3.16.
The first theorems relating to circles are attributed to Thales
around 650 BC. Book III of Euclid's Elementsdeals with
properties of circles and problems of inscribing and escribing polygons.
One of the problems of Greek mathematics was the problem of finding a
square with the same area as a given circle. Several of
the 'famous curves' in this stack were first studied in an attempt to
solve this problem. Anaxagoras in 450 BC is the first recored
mathematician to study this problem.
The problem of finding the area of a circle led to integration. For
the circle with formula given above the area is a2 and the
length of the curve is 2a.
The pedal of a circle is a cardioid if the pedal point is taken on
the circumference and is a limacon if the pedal point is not on the
circumference.
The caustic of a circle with radiant point on the circumference is a
cardioid, while if the rays are parallel then the caustic is a
nephroid.
Apollonius, in about 240 BC, showed effectively that the bipolar
equation r = kr' represents a system of coaxial circles as k
varies. In terms of bipolar equations mr2 + nr'2 = c2 represents a
circle whose centre divides the line segment between the two
fixed points of the system in the ratio n to m.
JOC/EFR/BS January 1997
The URL of this page is:
http://www-history.mcs.st-andrews.ac.uk/history/Curves/Circle.html
The brass tub in Solomon's temple was a
thick-sided vessel, and the measurement of ten cubits referred to the
outer diameter, while the measurement of thirty cubits referred to the
inner circumference. The thickness of the annulus was recorded as a
hand-breadth. If one considers a hand breadth to be 4 inches, and uses a
figure of 17.75 for a cubit, the value of p in the equation:
((10 - 30/p)/2)17.75
= 4
is p = 355/113.
I don't think the Hebrews calculated the values recorded,
merely observed them. The true value of
would give slightly different values for a hand-breadth and a cubit. I
think this fact is more interesting than the improper imputation of 3 as
the 'Biblical' value of .
Comment by: Bob Graf, 29th October 1996.
We note that the value 355/113 as an approximation for
was first noted by Tsu Ch'ung
Chi (430-501 AD)
Top of Page
